Understanding the Tensor Product through Monads

Note: This article presumes some prior knowledge of Monad/Functor/Applicative

I saw this on the Wikipedia page for Kronecker product:

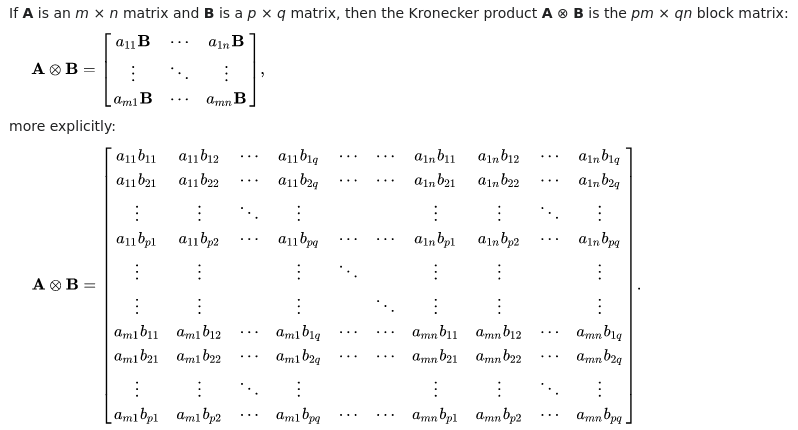
The first thought that came to my mind was “Hey, that looks like a Monad!” Specifically, multiplying every element of A by B, then flattening the result reminds me of the List Monad instance, where bind is equivalent to flatMap: first map the function a -> [b] to get a nested list [[b]], then flatten the nesting to get [b]. In the same way, the Kronecker product creates a series of nested matrices, which are then flattened into a normal 2D matrix by displaying each of the inner matrices in block format.

Let’s see if we can code it up in Haskell:

-- Matrix with unrestricted dimension
newtype Matrix a = Matrix { unMatrix :: [[a]] }

-- Show instance for convenience
instance Show a => Show (Matrix a) where
  show (Matrix m) = show m

-- fmap: map the function across every single element of the matrix
instance Functor Matrix where
  fmap f = Matrix . map (map f) . unMatrix

Here we define a Matrix type as a nested list, a Show instance for convenience, and a Functor instance where we define how to map a function across every element of a Matrix.

ghci> Matrix [[1,2],[3,4]]
[
  [1,2],
  [3,4]
]

-- Multiply every element by 10
ghci> fmap (*10) (Matrix [[1,2],[3,4]])
[
  [10,20],
  [30,40]
]

Here’s an illustration of the previous example:

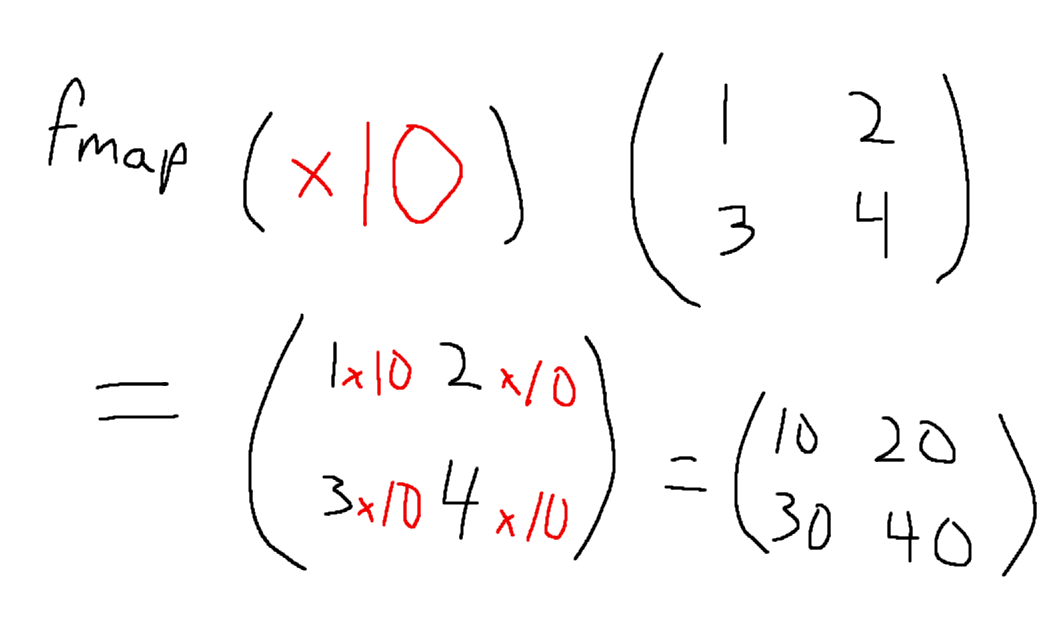
Now we get to Applicative instance. pure is easy – just make a single element matrix. But what about <*> :: f (a -> b) -> f a -> f b? How do we apply a Matrix of functions to a Matrix of single elements? It turns out that we can do exactly what is shown in the picture at the beginning of the article! We can simply apply each function we have in the Matrix:

blockedAp :: Matrix (a -> b) -> Matrix a -> Matrix (Matrix b)
blockedAp (Matrix ff) a = Matrix $
  for ff $ \row ->
    for row $ \f ->
      fmap f a

This function doesn’t get us fully there; it returns a nested Matrix (Matrix b), where the definition of <*> asks for a Matrix b. But this is just a block matrix:

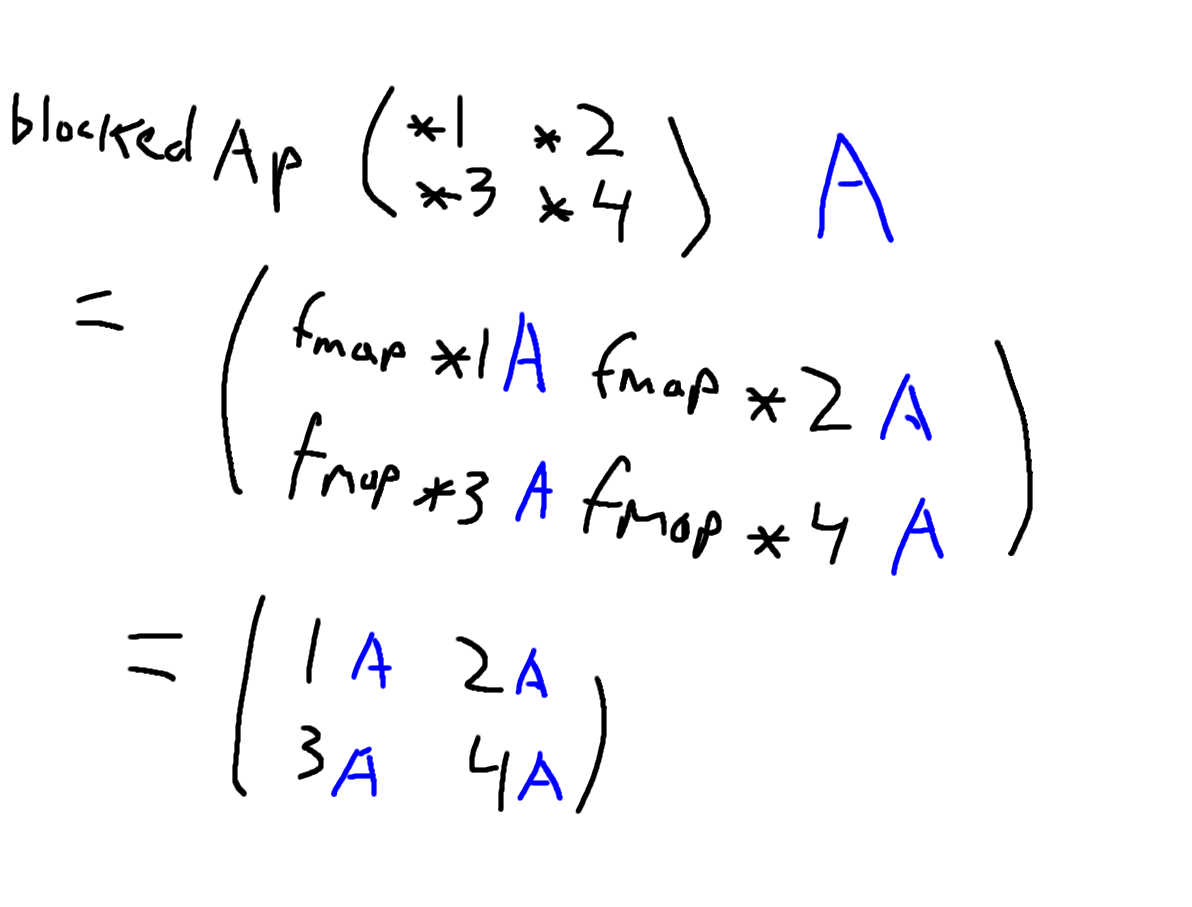
And just like in the Kronecker product, we can flatten the blocked matrix:

-- Flatten a block matrix
unblock :: Matrix (Matrix a) -> Matrix a
unblock (Matrix mm) = Matrix $ concatMap (foldl unblockRow []) mm
  where
  unblockRow [] (Matrix m) = m
  unblockRow acc (Matrix m) = zipWith (++) acc m

We can then put these together and get the Applicative instance.

instance Applicative Matrix where
  pure v = Matrix [[v]]
  (<*>) ff a = unblock (blockedAp ff a)

ghci> ff = Matrix [[(*2), (*3)], [(*4), (*5)]]
ghci> a = Matrix [[1, 10], [100, 1000]]
ghci> ff <*> a
[
  [2,20,3,30],
  [200,2000,300,3000],
  [4,40,5,50],
  [400,4000,500,5000]
]
ghci>

Now we can define the Kronecker product in terms of the Applicative:

ghci> kronecker a b = (fmap (*) a) <*> b
ghci> kronecker (Matrix [[2,4]]) a
[
  [2,20,4,40],
  [200,2000,400,4000]
]

But what about Monad? I tried to derive a Monad instance using unblock and fmap, but it’s not necessarily lawful, because the function argument to bind can return different matrix sizes for different inputs. For example:

ghci> let f x = if x == 0 then Matrix [[]] else Matrix [[1,2],[3,4]]
ghci> (Matrix [[0,2]] >>= f) >>= return
[[1,2]]
ghci> (Matrix [[0,2]]) >>= (\x -> f x >>= return)
[[1,2],[3,4]]

This violates the monad associativity law: (m >>= g) >>= h = m >>= (\x -> g x >>= return). So we have to settle for Applicative unless there’s a different, lawful definition.